7 Das LFKN Protokoll
Das LFKN Protokoll von Lund, Fortnow, Karloff und Nisan dient dazu die Korrektheit einer genannten Permanente einer Matrix zu beweisen. Merlin behauptet zu Beginn die Permanente der n x n Ausgangsmatrix M und will Arthur beweisen, dass diese korrekt ist. Dazu wird M in Untermatrizen zerlegt, von denen Merlin dann ebenfalls die Permanenten behaupten muß. Dies geschieht so lange, bis die Untermatrizen ein Größe von 1 x 1 erreicht haben. Für diese kann Arthur ganz einfach die Korrektheit der behaupteten Permanenten überprüfen.
Um von der Korrektheit der 1 x 1 Matrizen auf die Korrektheit der Ausgangsmatrix M schließen zu können, muß ein geeignetes Konsistenzkriterium verwendet werden. Hierfür wählt Arthur aus den Untermatrizen, die er von Merlin zusammen mit ihren Permanenten erhalten hat, zufällig zwei aus. Aus diesen beiden berechnet er eine neue Matrix D(x) = (1-x) M[i] + x M[j], für die Merlin wiederum die Permanente behaupten muß. Anschließend fasst Arthur die beiden gewählten Matrizen zu einer neuen Matrix zusammen, indem er ein zufälliges 1<r<N auswählt und dann D(r) berechnet. Dies geschieht so lange bis alle Untermatrizen zusammengefasst sind. Dann beginnt das Verfahren mit der zusammengefassten n-1 x n-1 großen Matrix als Ausgangsmatrix von vorne. Dies wiederholt sich so lange, bis die 1 x 1 Matrizen erreicht sind.
Hat Merlin nun an einer Stelle eine falsche Permanente behauptet, so muß er auch für alle folgenden Matrizen falsche Permanenten behaupten um nicht sofort als Lügner enttarnt zu werden. Spätestens bei den 1 x 1 Matrizen jedoch fliegt er auf, da dort eine falsche Permanente sofort festgestellt werden kann.
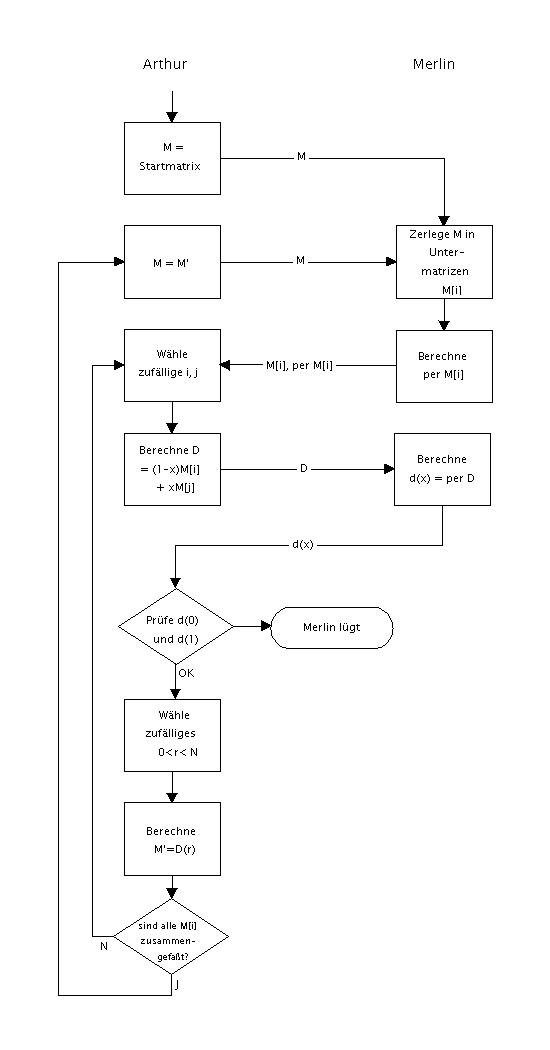
Ablaufdiagramm:

Das Applet lässt sich schrittweise ausführen, um den Ablauf des Algorithmus transparent zu machen:
|
Schritt |
Aktion |
|
1 |
Eingabedaten in Matrix M einlesen. |
|
2 |
Arthur sendet M an Merlin. Merlin bildet die Untermatrizen M[1] bis M[n] und berechnet deren Permanenten. |
|
3 |
Merlin sendet die Untermatrizen und die Permanenten an Arthur. Der bildet eine neue Matrix D aus zwei (zufällig ausgewählten) Untermatrizen: D = x * M[i] + (1-x) * M[j] |
|
4 |
Arthur sendet D an Merlin. Der berechnet die Permanente d(x) = per D. |
|
5 |
Merlin schickt d(x) an Arthur und der prüft d(0) = per M[j] und d(1) = per M[i] |
|
6 |
Arthur wählt ein zufälliges 0<r<N und berechnet ein neues M' = D(r). |
|
7 |
M' ersetzt M[i] und M[j], weiter mit Schritt 3 |
Applet LFKN:
Quellcode:
LFKN.java – Appletoberfläche und -steuerung, Aufruf der
einzelnen Schritte des Protokolls
Matrix.java – Double-Matrizen
Polynom.java – Polynome
PolynomMatrix.java – Polynom-Matrizen
(Matrizen, der Elemente Polynome sind)
 |
8 Visuelle Kryptographie |  |