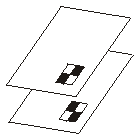
Für das 2 aus 2 Verfahren ergibt sich hier:
2 Folien, 1 Pixel mit je 4 Unterpixeln.
Überlagert ergibt sich schwarz, das Ausgangspixel ist also auch schwarz.
8 Visuelle Kryptographie
Die visuelle Kryptographie eignet sich zur Verschlüsselung und Geheimnisverteilung von Informationen die als schwarz-weiß Pixelbilder vorliegen. Dabei wird die Information auf mehrere transparente Folien verteilt, die durch Übereinanderlegen wieder die Information zurückliefern. Es sind beliebige Varianten mit k aus n Folien möglich, d.h. es werden k der n Folien benötigt um die Information zurückzuerhalten.
Jedes einzelne Pixel wird dabei in Unterpixel zerlegt, die so dicht beisammen liegen, dass das menschliche Auge sie als einzelnes Pixel wahrnimmt. Die Darstellung erfolgt als m x n Matrix S=[sij], wobei sij=1 ist, wenn das j-te Unterpixel in der i-ten Folie schwarz ist, sonst ist sij=0. Die Überlagerung der einzelnen Folien entspricht einer Oder-Verknüpfung der m Vektoren der Matrix.
Die Matrix für ein einzelnes schwarzes oder weißes Pixel wird bei der Verschlüsselung zufällig aus der Menge C0 für weiße Pixel bzw. C1 für schwarze Pixel gewählt. Die Mengen C0 und C1 enthalten alle Matrizen, die durch die Permutation der Spalten je einer Ausgangsmatrix für schwarze und weiße Pixel, entstehen. Die verwendete Ausgangsmatrix ist abhängig von der gewünschten Anzahl Folien (n aus k). Die Matrix für weiße Pixel muss so gewählt werden, dass die Oder-Verknüpfung (Überlagerung) immer einen Grauwert liefert, den das Auge noch deutlich von Schwarz unterscheiden kann. Die Matrix für schwarze Pixel wird so gewählt, das die Oder-Verknüpfung von mindestens k Folien den Wert Schwarz ergibt, und die Verknüpfung von weniger als k Folien einen Grauwert, der sich nicht von der Verknüpfung der weißen Pixel unterscheidet, so dass bei weniger als k Folien keine Information sichtbar wird.
Im folgenden Beispiel ist ein 2 aus 2 Verfahren implementiert.
|
|
Für das 2 aus 2 Verfahren ergibt sich hier: |
Als Matrizen für dieses Verfahren wären folgende ausreichend:
C0 = alle Spalten-Permutationen von ![]()
C1 = alle Spalten-Permutationen von ![]()
In der Praxis ergibt sich aber das Problem, dass dabei nur 2 Unterpixel für
jedes Pixel erzeugt würden. Dadurch würde das Bild verzerrt werden. Man
verwendet daher folgende Matrizen, die 4 Unterpixel für jedes Pixel erzeugen:
C0 = alle Spalten-Permutationen von ![]()
C1 = alle Spalten-Permutationen von ![]()
Applet visuelle Kryptographie
Ziehen Sie mit der Maus das rechte Teilgeheimnisbild auf das linke!
Quellcode:
vc.java