7 The LFKN protocol
The LFKN protocol was written by Lund, Fort, Karloff and Nisan to proof the correctness of a claimed permanent of a matrix. At first Merlin claims the permanent of a n x n matrix M and tries to proof Arthur, that it is correct. To do this, he has to split M into submatrices and claim the permanents of those as well. This continues until the submatrices reach the size of 1 x 1. For those Arthur can easily check the correctness of the permanents.
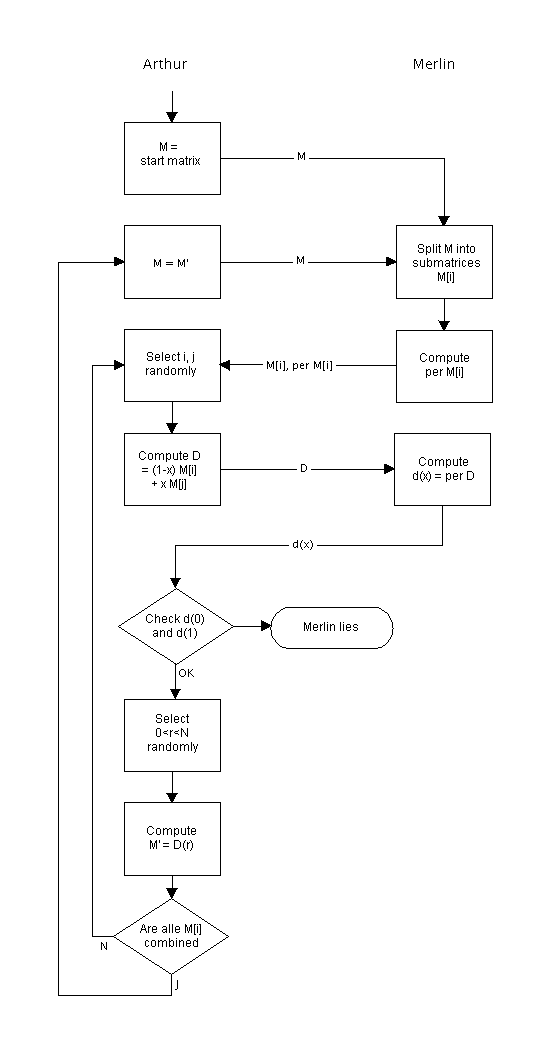
To conculde from the correctness of the 1 x 1 matrices to the correctness of the first matrix M, a suitable consitency criterion as to be used. To achieve this, Arthur randomly selects two of the submatrices he got from Merlin together with their claimed permanents. He then computes one new matrix from those two. D(x) = (1-x) M[i] + x M[j]. Then he sends D(x) back to Merlin, who has to claim the permanent of this matrix as well. After that Arthur combines the two selected matrices to one by randomly choosing an value 1<r<N and the computing D(r). This continues until all of the submatrices have been combined to one single matrix. After that the whole process starts again with the last combined matrix of size n-1 x n-1. And this continues until there are only 1 x 1 matrices left.
If Merlin has falsely claimed a permanent at one point, he has claim wrong ones for all the matrices that follow, not to be caught lying at once. But in the end he would be cought in any case, because the permanent of a 1 x 1 matrix is easly checked.
Flowchart:

The applet runs in single steps to make the algorithm more transparent:
|
step |
action |
|
1 |
Read values from input matrix M. |
|
2 |
Arthur sends M to Merlin. Merlin builds submatrices M[1] to M[n] and computes their permanents. |
|
3 |
Merlin sends the submatrices and their permanents to Arthur. Arthur computes a new matrix D from two randomly selected submatrices D = x * M[i] + (1-x) * M[j] |
|
4 |
Arthur sends D to Merlin. Merlin claims the permanant d(x) = per D. |
|
5 |
Merlin sends d(x) to Arthur, who checks d(0) = per M[j] and d(1) = per M[i] |
|
6 |
Arthur randomly selects 0<r<N and computes a new matrix M' = D(r). |
|
7 |
Subsitute M[i] and M[j] with M'. Continue with step 3. |
Applet LFKN:
Sourcecode:
LFKN.java – Applet GUI
Matrix.java – Double-Matrices
Polynom.java – Polynoms
PolynomMatrix.java – Polynom-Matrices
 |
8 Visual cryptography |  |