LogCFL

LogCFL is the class of problems logspace-reducible to a context-free language. Two important and useful characterizations of this class are summarized in the following proposition. (SAC and AuxPDA are defined in the following paragraphs.)

An Auxiliary Pushdown Automaton (AuxPDA) is a nondeterministic Turing machine with a read-only input tape, a space-bounded worktape, and a pushdown store that is not subject to the space-bound. The class of languages accepted by Auxiliary Pushdown Automata in space s(n) and time t(n) is denoted by AuxPDA(s(n),t(n)). If an AuxPDA satisfies the property that, on every input x, there is at most one accepting computation, then the AuxPDA is said to be unambiguous. This gives rise to the class UAuxPDA(s(n),t(n)).

SAC is the class of languages accepted by logspace-uniform semi-unbounded circuits of depth ; a circuit family is semi-unbounded if the AND gates have fan-in 2 and the OR gates have unbounded fan-in.

Not long after NL was shown to be closed under complementation [Imm88, Sze88], LogCFL was also shown to be closed under complementation in a proof that also used the inductive counting technique ([BCD 89]). A similar history followed a few years later: not long after it was shown that NL is contained in L/poly [Wig94, GW96], the isolation lemma was again used to show that LogCFL is contained in SAC /poly [Gál95, GW96]. (As is noted in [GW96], this was independently shown by H. Venkateswaran.)

In this section, we show that the same techniques that were used in Section can be used to prove an analogous result about LogCFL. (In fact, it would also be possible to derive the result of Section from a modification of the proof of this section. Since some readers may be more interested in NL than LogCFL, we have chosen to present a direct proof of NL/poly = UL/poly.) The first step is to state the analog to Lemma . Before we can do that, we need some definitions.

A weighted circuit is a semiunbounded circuit together with a weighting function that assigns a nonnegative integer weight to each wire connecting any two gates in the circuit.

Let C be a weighted circuit, and let g be a gate of C. A certificate for g(x) = 1 (in C) is a list of gates, corresponding to a depth-first search of the subcircuit of C rooted at g. The weight of a certificate is the sum of the weights of the edges traversed in the depth-first search. This informal definition is made precise by the following inductive definition. (It should be noted that this definition differs in some unimportant ways from the definition given in [Gál95, GW96].)

• If g is a constant 1 gate or an input gate evaluating to 1 on input x, then the only certificate for g is the string g. This certificate has weight 0.
• If g is an AND gate of C with inputs and (where lexicographically precedes ), then any string of the form gyz is a certificate for g, where y is any certificate for , and z is any certificate for . If is the weight of the edge connecting to g, then the weight of the certificate yz is plus the sum of the weights of certificates y and z.
• If g is an OR gate of C, then any string of the form gy is a certificate for g, where y is any certificate for a gate h that is an input to g in C. If w is the weight of the edge connecting h to g, then the weight of the certificate gy is w plus the weight of certificate y.

Note that if C has logarithmic depth d, then any certificate has length bounded by a polynomial in n and has weight bounded by times the maximum weight of any edge. Every gate that evaluates to 1 on input x has a certificate, and no gate that evaluates to 0 has a certificate.

We will say that a weighted circuit C is min-unique on input x if, for every gate g that evaluates to 1 on input x, the minimal-weight certificate for g(x) = 1 is unique.

 

Lemma is in some sense implicit in [Gál95, GW96]. We include a proof for completeness.

Proof: Let A be in LogCFL, and let C be the semiunbounded circuit of size and depth recognizing A on inputs of length n.

As in [Gál95, GW96], a modified application of the isolation lemma technique of [MVV87] shows that, for each input x, if each wire in C is assigned a weight in the range uniformly and independently at random, then with probability at least , C is min-unique on input x. (Sketch: The probability that there is more than one minimum weight certificate for g(x) = 1 is bounded by the sum, over all wires e, of the probability of the event BAD(e,g) ::= ``e occurs in one minimum-weight certificate for g(x) = 1 and not in another''. Given any weight assignment w' to the edges in C other than e, there is at most one value z with the property that, if the weight of e is set to be z, then BAD(e,g) occurs. Thus the probability that there are two minimum-weight certificates for any gate in C is bounded by = .)

Now consider sequences consisting of n weight functions , where each weight function assigns a weight in the range to each edge of C. (There are such sequences possible for each n.) There must exist a string such that, for each input x of length n, there is some such that the weighted circuit that results by applying weight function to C is min-unique on input x. (Sketch of proof: Let us call a sequence ``bad for x'' if none of the circuits in the sequence is min-unique on input x. For each x, the probability that a randomly-chosen is bad is bounded by (probability that is not min-unique) . Thus the total number of sequences that are bad for some x is at most . Thus there is some sequence that is not bad.)

The desired advice sequence is formed by taking a good sequence and letting be the result of applying weight function to C.

Proof: Let A be a language in LogCFL. Let x be a string of length n, and let be the advice sequence guaranteed by Lemma .

We show that there is an unambiguous auxiliary pushdown automaton M that runs in polynomial time and uses logarithmic space on its worktape that, given a sequence of circuits as input, processes each circuit in turn, and has the following properties:

• If is not min-unique on input x, then M has a unique path that determines this fact and goes on to process ; all other paths are rejecting.
• If is min-unique on input x and evaluates to 1 on input x, then M has a unique accepting path.
• If is min-unique on input x but evaluates to zero on input x, then M has no accepting path.

Our construction is similar in many respects to that of Section . Given a circuit C, let denote the number of gates g that have a certificate for g(x)=1 of weight at most k, and let be the sum, over all gates g having a certificate for g(x) = 1 of weight at most k, of the minimum-weight certificate of g. (Let W(g) denote the weight of the minimum-weight certificate of g(x) = 1, if such a certificate exists, and let this value be otherwise.)

A useful observation is that if all gates of C having certificates of weight at most k have unique minimal-weight certificates (and if the correct values of and are provided), then an unambiguous AuxPDA can, on input , compute the Boolean value of the predicate `` ''. This is achieved with the routine shown in Figure .

  
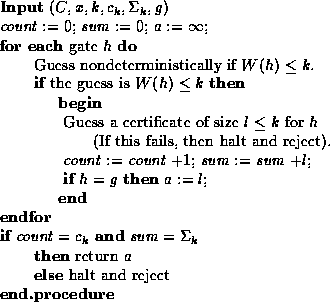
Figure: An unambiguous routine to calculate W(g) if and return otherwise.

To see that this routine truly is unambiguous if the preconditions are met, note the following:

• If the routine ever guesses incorrectly for some gate h that W(h) > k, then the variable count will never reach and the routine will reject. Thus the only paths that run to completion guess correctly exactly the set .
• For each gate h such that , there is exactly one minimal-weight certificate that can be found. An UAuxPDA will find this certificate using its pushdown to execute a depth-first search (using nondeterminism at the OR gates, and using its workspace to compute the weight of the certificate), and only one path will find the the minimal-weight certificate. If, for some gate h, a certificate of weight greater than W(h) is guessed, then the variable sum will not be equal to at the end of the routine, and the path will halt and reject.

Clearly, all gates at the input level have unique minimal-weight certificates (and the only gates g with W(g)= 0 are at the input level). Thus we can set (since each input bit and its negation are provided, along with the constant 1), and . A key part of the construction involves computing and from , at the same time checking that no gate has two minimal-weight certificates of weight k. Consider each gate g in turn. If g is an AND gate with inputs and and weights and connecting g to these inputs, then if and only if or ((W(g) > k-1) and ( )). If g is an OR gate, then it suffices to check, for each gate h that is connected to g by an edge of weight w, if or ((W(g) > k-1) and (W(h)+w=k)); if one such gate is found, then W(g) = k; if two such gates are found, then the circuit is not min-unique on input x. If no violations of this sort are found for any k, then C is min-unique on input x. The code shown in Figure formalizes these considerations.

  
Figure: Computing and .

Evaluating a given circuit is now expressed by the routine shown in Figure .

  
Figure: Evaluating a circuit.

Given the sequence , the routine processes each in turn. If is not is min-unique on input x, then one unique computation path of the routine returns the value BAD.CIRCUIT and goes on to process ; all other computation paths halt and reject. Otherwise, the routine has a unique accepting path if , and if this is not the case the routine halts with no accepting computation paths.