


Next: About this document
Up: Making Nondeterminism Unambiguous
Previous: Discussion and Open Problems
References
- ABO96
-
E. Allender, R. Beals, and M. Ogihara.
The complexity of matrix rank and feasible systems of linear
equations.
In ACM Symposium on Theory of Computing (STOC), 1996.
- AJ93
-
C. Àlvarez and B. Jenner.
A very hard log-space counting class.
Theoretical Computer Science, 107:3-30, 1993.
- AL96
-
E. Allender and K.-J. Lange.
StUSPACE(
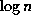 ) is contained in DSPACE(
) is contained in DSPACE( 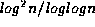 ).
In Proceedings of the 7th ACM-SIGSAM International Symposium on
Symbolic and Algebraic Computation (ISAAC), volume 1178 of Lecture
Notes in Computer Science, pages 193-202. Springer-Verlag, 1996.
).
In Proceedings of the 7th ACM-SIGSAM International Symposium on
Symbolic and Algebraic Computation (ISAAC), volume 1178 of Lecture
Notes in Computer Science, pages 193-202. Springer-Verlag, 1996.
- AO96
-
E. Allender and M. Ogihara.
Relationships among PL, #L and the determinant.
RAIRO - Theoretical Information and Application, 30:1-21,
1996.
- BCD
 89
89 -
A. Borodin, S. A. Cook, P. W. Dymond, W. L. Ruzzo, and M. Tompa.
Two applications of inductive counting for complementation problems.
SIAM Journal on Computing, 18(3):559-578, 1989.
- BF
-
R. Beigel and B. Fu.
Circuits over PP and PL.
To appear in Proceedings of the 12th Conference on Computational
Complexity, 1997.
- BJLR92
-
G. Buntrock, B. Jenner, K.-J. Lange, and P. Rossmanith.
Unambiguity and fewness for logarithmic space.
In Proc. 8th International Conference on Fundamentals of
Computation Theory (FCT '91), volume 529 of Lecture Notes in Computer
Science, pages 168-179. Springer-Verlag, 1992.
- Dam
-
C. Damm.
DET = L
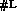 ?
Informatik-Preprint 8, Fachbereich Informatik der
Humboldt-Universität zu Berlin, 1991.
?
Informatik-Preprint 8, Fachbereich Informatik der
Humboldt-Universität zu Berlin, 1991.
- Gál95
-
A. Gál.
Semi-unbounded fan-in circuits: Boolean vs. arithmetic.
In IEEE Structure in Complexity Theory Conference, pages
82-87, 1995.
- GS88
-
J. Grollmann and A. Selman.
Complexity measures for public-key cryptosystems.
SIAM Journal on Computing, 17:309-335, 1988.
- GW96
-
A. Gál and A. Wigderson.
Boolean vs. arithmetic complexity classes: randomized reductions.
Random Structures and Algorithms, 9:99-111, 1996.
- Imm88
-
N. Immerman.
Nondeterministic space is closed under complement.
SIAM Journal on Computing, 17:935-938, 1988.
- Jon75
-
N. D. Jones.
Space bounded reducibility among combinatorial problems.
Journal of Computer and System Sciences, 11:68-85, 1975.
- MV97
-
M. Mahajan and V. Vinay.
A combinatorial algorithm for the determinant.
In Proceedings of the Eighth Annual ACM-SIAM Symposium on
Discrete Algorithms (SODA), 1997.
- MVV87
-
K. Mulmuley, U. Vazirani, and V. Vazirani.
Matching is as easy as matrix inversion.
Combinatorica, 7:105-113, 1987.
- NR95
-
R. Niedermeier and P. Rossmanith.
Unambiguous auxiliary pushdown automata and semi-unbounded fan-in
circuits.
Information and Computation, 118(2):227-245, 1995.
- Ogi96
-
M. Ogihara.
The PL hierarchy collapses.
In ACM Symposium on Theory of Computing (STOC), pages 84-88,
1996.
- RR92
-
P. Rossmanith and W. Rytter.
Observations on
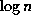 time parallel recognition of unambiguous
context-free languages.
Information Processing Letters, 44:267-272, 1992.
time parallel recognition of unambiguous
context-free languages.
Information Processing Letters, 44:267-272, 1992.
- Ryt87
-
W. Rytter.
Parallel time O(
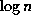 ) recognition of unambiguous context-free
languages.
Information and Computation, 73:75-86, 1987.
) recognition of unambiguous context-free
languages.
Information and Computation, 73:75-86, 1987.
- Sud78
-
I. H. Sudborough.
On the tape complexity of deterministic context-free languages.
J. Association of Computing Machinery, 25:405-414, 1978.
- Sze88
-
R. Szelepcsényi.
The method of forced enumeration for nondeterministic automata.
Acta Informatica, 26:279-284, 1988.
- Tod
-
S. Toda.
Counting problems computationally equivalent to the determinant.
Technical Report CSIM 91-07, Department of Computer Science and
Information Mathematics, University of Electro-Communications, Tokyo, 1991.
- Val76
-
L. Valiant.
The relative complexity of checking and evaluating.
Information Processing Letters, 5:20-23, 1976.
- Val92
-
L. Valiant.
Why is Boolean complexity theory difficult?
In M. Paterson, editor, Boolean Function Complexity, volume
169 of London Mathematical Society Lecture Notes Series, pages 84-94.
Cambridge University Press, 1992.
- Ven91
-
Venkateswaran.
Properties that characterize LOGCFL.
Journal of Computer and System Sciences, 43, 1991.
- Vin91
-
V. Vinay.
Counting auxiliary pushdown automata and semi-unbounded arithmetic
circuits.
In Proc. 6th Structure in Complexity Theory Conference, pages
270-284. IEEE, 1991.
- VV86
-
L. Valiant and V. Vazirani.
NP is as easy as detecting unique solutions.
Theoretical Computer Science, 47:85-93, 1986.
- Wig94
-
A. Wigderson.
NL/poly
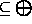 L/poly.
In Proc. of the 9th IEEE Structure in Complexity Conference,
pages 59-62, 1994.
L/poly.
In Proc. of the 9th IEEE Structure in Complexity Conference,
pages 59-62, 1994.
Klaus Reinhardt
Mon Apr 28 16:41:00 MST 1997