LogCFL is the class of problems logspace-reducible to a context-free
language. Two important and useful characterizations of this class
are summarized in the following proposition.
(SAC ![]() and AuxPDA
and AuxPDA ![]() are defined in the following
paragraphs.)
are defined in the following
paragraphs.)
![]()
An Auxiliary Pushdown Automaton (AuxPDA) is a nondeterministic Turing machine with a read-only input tape, a space-bounded worktape, and a pushdown store that is not subject to the space-bound. The class of languages accepted by Auxiliary Pushdown Automata in space s(n) and time t(n) is denoted by AuxPDA(s(n),t(n)). If an AuxPDA satisfies the property that, on every input x, there is at most one accepting computation, then the AuxPDA is said to be unambiguous. This gives rise to the class UAuxPDA(s(n),t(n)).
SAC ![]() is the class of languages accepted
by logspace-uniform semi-unbounded circuits of depth
is the class of languages accepted
by logspace-uniform semi-unbounded circuits of depth ![]() ;
a circuit family is semi-unbounded if the AND gates have fan-in 2 and
the OR gates have unbounded fan-in.
;
a circuit family is semi-unbounded if the AND gates have fan-in 2 and
the OR gates have unbounded fan-in.
Not long after NL was shown to be closed under complementation
[Imm88, Sze88], LogCFL was also shown to be closed under complementation
in a proof that also used the inductive counting technique
([BCD ![]() 89]). A similar history followed a few years later: not long
after it was shown that NL is contained in
89]). A similar history followed a few years later: not long
after it was shown that NL is contained in ![]() L/poly [Wig94, GW96],
the isolation lemma was again used to show that
LogCFL is contained in
L/poly [Wig94, GW96],
the isolation lemma was again used to show that
LogCFL is contained in ![]() SAC
SAC ![]() /poly [Gál95, GW96].
(As is noted in [GW96], this was independently shown by
H. Venkateswaran.)
/poly [Gál95, GW96].
(As is noted in [GW96], this was independently shown by
H. Venkateswaran.)
In this section, we show that the same techniques that were used
in Section ![]() can be used to prove an analogous result
about LogCFL. (In fact, it would also be possible to derive the result
of Section
can be used to prove an analogous result
about LogCFL. (In fact, it would also be possible to derive the result
of Section ![]() from a modification of the proof of this section.
Since some readers may be more interested in NL than LogCFL, we have
chosen to present a direct proof of NL/poly = UL/poly.)
The first step is to state the analog to Lemma
from a modification of the proof of this section.
Since some readers may be more interested in NL than LogCFL, we have
chosen to present a direct proof of NL/poly = UL/poly.)
The first step is to state the analog to Lemma ![]() .
Before we can do that, we need some definitions.
.
Before we can do that, we need some definitions.
A weighted circuit is a semiunbounded circuit together with a weighting function that assigns a nonnegative integer weight to each wire connecting any two gates in the circuit.
Let C be a weighted circuit, and let g be a gate of C. A certificate for g(x) = 1 (in C) is a list of gates, corresponding to a depth-first search of the subcircuit of C rooted at g. The weight of a certificate is the sum of the weights of the edges traversed in the depth-first search. This informal definition is made precise by the following inductive definition. (It should be noted that this definition differs in some unimportant ways from the definition given in [Gál95, GW96].)
We will say that a weighted circuit C is min-unique on input x if, for every gate g that evaluates to 1 on input x, the minimal-weight certificate for g(x) = 1 is unique.
Lemma ![]() is in some sense implicit in [Gál95, GW96]. We
include a proof for completeness.
is in some sense implicit in [Gál95, GW96]. We
include a proof for completeness.
Proof: Let A be in LogCFL, and let C be the semiunbounded circuit
of size ![]() and depth
and depth ![]() recognizing A on inputs of length n.
recognizing A on inputs of length n.
As in [Gál95, GW96], a modified application of the isolation
lemma technique of [MVV87] shows that, for each input
x, if each wire in
C is assigned a weight in the range ![]() uniformly and
independently at random, then with probability at least
uniformly and
independently at random, then with probability at least
![]() , C is min-unique on input x.
(Sketch: The probability that there
is more than one minimum weight certificate for g(x) = 1 is bounded
by the sum, over all wires e, of the probability of the event
BAD(e,g) ::= ``e occurs in one minimum-weight certificate
for g(x) = 1 and not in another''.
Given any weight assignment w' to the edges in C other than
e, there is at most one value z with the property that,
if the weight of e is set to be z, then BAD(e,g) occurs.
Thus the probability that there are two minimum-weight certificates
for any gate in C is bounded by
, C is min-unique on input x.
(Sketch: The probability that there
is more than one minimum weight certificate for g(x) = 1 is bounded
by the sum, over all wires e, of the probability of the event
BAD(e,g) ::= ``e occurs in one minimum-weight certificate
for g(x) = 1 and not in another''.
Given any weight assignment w' to the edges in C other than
e, there is at most one value z with the property that,
if the weight of e is set to be z, then BAD(e,g) occurs.
Thus the probability that there are two minimum-weight certificates
for any gate in C is bounded by
![]()
![]()
![]() =
=
![]() .)
.)
Now consider sequences ![]() consisting of n
weight functions
consisting of n
weight functions ![]() ,
where each weight function assigns a weight
in the range
,
where each weight function assigns a weight
in the range ![]() to each edge of C.
(There are
to each edge of C.
(There are ![]() such sequences possible for each n.)
There must exist a string
such sequences possible for each n.)
There must exist a string ![]() such that, for each
input x of length n, there is some
such that, for each
input x of length n, there is some ![]() such that
the weighted circuit
such that
the weighted circuit ![]() that results by applying weight function
that results by applying weight function
![]() to C is min-unique on input x.
(Sketch of proof:
Let us call a sequence
to C is min-unique on input x.
(Sketch of proof:
Let us call a sequence ![]() ``bad for x'' if none of the circuits
``bad for x'' if none of the circuits
![]() in the sequence is min-unique on input x.
For each x,
the probability that a randomly-chosen
in the sequence is min-unique on input x.
For each x,
the probability that a randomly-chosen ![]() is
bad is bounded by (probability that
is
bad is bounded by (probability that ![]() is not min-unique)
is not min-unique) ![]()
![]() . Thus the total number of sequences
that are bad for some x is at most
. Thus the total number of sequences
that are bad for some x is at most ![]() .
Thus there is some sequence
.
Thus there is some sequence ![]() that is not bad.)
that is not bad.)
The desired advice sequence ![]() is formed by taking a good sequence
is formed by taking a good sequence ![]() and letting
and letting ![]() be the result of applying weight function
be the result of applying weight function ![]() to
C.
to
C.
![]()
Proof: Let A be a language in LogCFL. Let x be a string of length
n, and let ![]() be the advice sequence
guaranteed by Lemma
be the advice sequence
guaranteed by Lemma ![]() .
.
We show that there is an unambiguous auxiliary pushdown automaton M that runs in polynomial time and uses logarithmic space on its worktape that, given a sequence of circuits as input, processes each circuit in turn, and has the following properties:
Our construction is similar in many respects to that of Section
![]() . Given a circuit C, let
. Given a circuit C, let ![]() denote the number
of gates g that have a certificate for g(x)=1
of weight at most k, and let
denote the number
of gates g that have a certificate for g(x)=1
of weight at most k, and let
![]() be the sum, over all gates g having a certificate for
g(x) = 1
of weight at most k, of the minimum-weight certificate of g.
(Let W(g) denote the weight of the minimum-weight certificate
of g(x) = 1, if such a certificate exists, and let this value
be
be the sum, over all gates g having a certificate for
g(x) = 1
of weight at most k, of the minimum-weight certificate of g.
(Let W(g) denote the weight of the minimum-weight certificate
of g(x) = 1, if such a certificate exists, and let this value
be ![]() otherwise.)
otherwise.)
A useful observation is that if all gates of C having certificates
of weight at most k have unique minimal-weight certificates (and if the
correct values of ![]() and
and ![]() are provided), then
an unambiguous AuxPDA can, on input
are provided), then
an unambiguous AuxPDA can, on input ![]() ,
compute the Boolean value of the predicate ``
,
compute the Boolean value of the predicate `` ![]() ''.
This is achieved with the routine shown in Figure
''.
This is achieved with the routine shown in Figure ![]() .
.
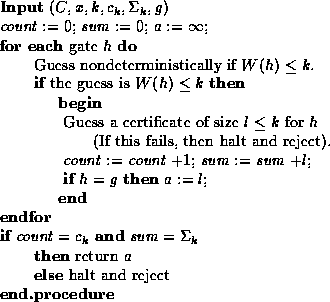
Figure: An unambiguous routine to calculate W(g)
if ![]() and return
and return ![]() otherwise.
otherwise.
To see that this routine truly is unambiguous if the preconditions are met, note the following:
Clearly, all gates at the input level have unique minimal-weight
certificates (and the only gates g with W(g)= 0 are at the
input level). Thus we can set
![]() (since each
input bit and its negation are provided, along with the constant 1),
and
(since each
input bit and its negation are provided, along with the constant 1),
and ![]() .
A key part of the construction involves computing
.
A key part of the construction involves computing ![]() and
and ![]() from
from ![]() , at the same time
checking that no gate has two minimal-weight certificates of weight
k. Consider each gate g in turn.
If g is an AND gate with inputs
, at the same time
checking that no gate has two minimal-weight certificates of weight
k. Consider each gate g in turn.
If g is an AND gate with inputs ![]() and
and ![]() and weights
and weights ![]() and
and ![]() connecting g to these inputs, then
connecting g to these inputs, then ![]() if and only if
if and only if ![]() or ((W(g) > k-1) and
(
or ((W(g) > k-1) and
( ![]() )).
If g is an OR gate, then it suffices to check, for each gate
h that is connected to g by an edge of weight w, if
)).
If g is an OR gate, then it suffices to check, for each gate
h that is connected to g by an edge of weight w, if
![]() or ((W(g) > k-1) and (W(h)+w=k));
if one such gate is found, then W(g) = k; if two such gates are found, then
the circuit is not min-unique on input
x. If no violations of this sort are found for any k, then C
is min-unique on input x.
The code shown in Figure
or ((W(g) > k-1) and (W(h)+w=k));
if one such gate is found, then W(g) = k; if two such gates are found, then
the circuit is not min-unique on input
x. If no violations of this sort are found for any k, then C
is min-unique on input x.
The code shown in Figure ![]() formalizes these considerations.
formalizes these considerations.
Evaluating a given circuit ![]() is now expressed by the
routine shown in Figure
is now expressed by the
routine shown in Figure ![]() .
.
Given the sequence ![]() , the routine processes
each
, the routine processes
each ![]() in turn. If
in turn. If ![]() is not is min-unique
on input x, then one unique computation path of the
routine returns the value BAD.CIRCUIT and goes on to process
is not is min-unique
on input x, then one unique computation path of the
routine returns the value BAD.CIRCUIT and goes on to process ![]() ;
all other computation paths halt and reject.
Otherwise, the routine has a unique
accepting path if
;
all other computation paths halt and reject.
Otherwise, the routine has a unique
accepting path if ![]() , and if this is not the case
the routine halts with no accepting computation paths.
, and if this is not the case
the routine halts with no accepting computation paths.
![]()