Nondeterministic Logspace

 

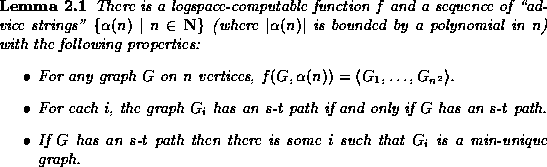
The s-t connectivity problem takes as input a directed graph with two distinguished vertices s and t, and determines if there is a path in the graph from s to t. It is well-known that this is a complete problem for NL [Jon75].

The following lemma is implicit in [Wig94, GW96], but for completeness we make it explicit here.

 

Proof: We first observe that a standard application of the isolation lemma technique of [MVV87] shows that, if each edge in G is assigned a weight in the range uniformly and independently at random, then with probability at least , for any two vertices x and y such that there is a path from x to y, there is only one path having minimum weight. (Sketch: The probability that there is more than one minimum weight path from x to y is bounded by the sum, over all edges e, of the probability of the event BAD(e,x,y) ::= ``e occurs on one minimum-weight path from x to y and not in another''. Given any weight assignment w' to the edges in G other than e, there is at most one value z with the property that, if the weight of e is set to be z, then BAD(e,x,y) occurs. Thus the probability that there are two minimum-weight paths between two vertices is bounded by = .)

Our advice string will consist of a sequence of weight functions, where each weight function assigns a weight in the range to each edge. (There are such advice strings possible for each n.) Our logspace-computable function f takes as input a graph G and a sequence of weight functions, and produces as output a sequence of graphs , where graph is the result of replacing each edge e = (x,y) in G by a path of length j from x to y, where j is the weight given to e by the i-th weight function in the advice string. Note that, if the i-th weight function satisfies the property that there is at most one minimum weight path between any two vertices, then is a min-unique graph. (It suffices to observe that, for any two vertices x and y of , there are vertices x' and y' such that

• x' and y' are vertices of the original graph G, and they lie on every path between x and y,
• there is only one path from x to x', and only one path from y' to y, and
• the minimum weight path from x to y is unique.)

Let us call an advice string ``bad for G'' if none of the graphs in the sequence f(G) is a min-unique graph. For each G, the probability that a randomly-chosen advice string is bad is bounded by (probability that is not min-unique) . Thus the total number of advice strings that are bad for some G is at most . Thus there is some advice string that is not bad.

Proof: It suffices to present a UL/poly algorithm for the s-t connectivity problem.

We show that there is a nondeterministic logspace machine M that takes as input a sequence of digraphs , and processes each in sequence, with the following properties:

• If is not min-unique, M has a unique path that determines this fact and goes on to process ; all other paths are rejecting.
• If is a min-unique graph with an s-t path, then M has a unique accepting path.
• If is a min-unique graph with no s-t path, then M has no accepting path.

Combining this routine with the construction of Lemma yields the desired UL/poly algorithm.

Our algorithm is an enhancement of the inductive counting technique of [Imm88] and [Sze88]. We call this the double counting technique since in each stage we count not only the number of vertices having distance at most k from the start vertex, but also the sum of the lengths of the shortest path to each such vertex. In the following description of the algorithm, we denote these numbers by and , respectively.

Let us use the notation d(v) to denote the length of the shortest path in a graph G from the start vertex to v. (If no such path exists, then d(v) = n+1.) Thus, using this notation, .

A useful observation is that if the subgraph of G having distance at most k from the start vertex is min-unique (and if the correct values of and are provided), then an unambiguous logspace machine can, on input , compute the Boolean predicate `` ''. This is achieved with the routine shown in Figure .

  
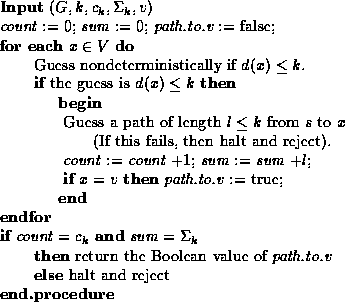
Figure: An unambiguous routine to determine if .

To see that this routine truly is unambiguous if the preconditions are met, note the following:

• If the routine ever guesses incorrectly for some vertex x that d(x) > k, then the variable count will never reach and the routine will reject. Thus the only paths that run to completion guess correctly exactly the set .
• If the routine ever guesses incorrectly the length l of the shortest path to x, then if d(x) > l no path of length l will be found, and if d(x) < l then the variable sum will be incremented by a value greater than d(x). In the latter case, at the end of the routine, will be greater than , and the routine will reject.

Clearly, the subgraph having distance at most 0 from the start vertex is min-unique, and and . A key part of the construction involves computing and from and , at the same time checking that the subgraph having distance at most k from the start vertex is min-unique. It is easy to see that is equal to plus the number of vertices having d(v) = k. Note that d(v) = k if and only if it is not the case that and there is some edge (x,v) such that . The graph fails to be a min-unique graph if and only if there exist some v and x as above, as well as some other such that and there is an edge (x',v). The code shown in Figure formalizes these considerations.

  
Figure: Computing and .

Searching for an s-t path in graph G is now expressed by the routine shown in Figure .

  
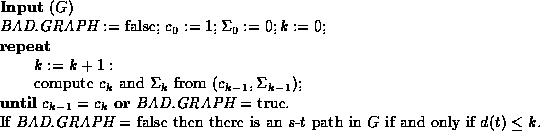
Figure: Finding an s-t path in a min-unique graph.

Given the sequence , the routine processes each in turn. If is not min-unique (or more precisely, if the subgraph of that is reachable from the start vertex is not a min-unique graph), then one unique computation path of the routine returns the value BAD.GRAPH and goes on to process ; all other computation paths halt and reject. Otherwise, if is min-unique, the routine has a unique accepting path if has an s-t path, and if this is not the case the routine halts with no accepting computation paths.