4.5.5 Shamirs Algorithmus

Im Jahr 1982 hat Shamir einen Algorithmus veröffentlicht, der das Ende des Merkle-Hellman Kryptosystems bedeutete [SH82]. Der Algorithmus versucht, aus einem gegebenen öffentlichen Schlüssel B ein Paar (U, M) zu ermitteln. Mit dem Paar (U, M) und B kann eine superansteigende Folge A konstruiert und somit jede Nachricht entschlüsselt werden, die zuvor mit B chiffriert wurde. Das Paar (U, M) ist ein Trapdoor-Paar.

Erinnerung:
Ein Merkle-Hellman Schlüsselpaar wird erzeugt, indem eine superansteigende Folge A = (a₁, ..., a_n), ein Modulus M mit M > a₁ + ... + a_n sowie eine weitere Zahl W < M mit ggT(M, W) = 1 gewählt werden. Da W relativ prim zu M ist, existiert eine Zahl U < M mit UW = 1 (mod M). Das Tupel (A, M, W) bildet den privaten Schlüssel. Der öffentliche Schlüssel wird durch die Vorschrift b_i = a_iW mod M ermittelt.

Umgekehrt lassen sich die Komponenten von A durch a_i = b_iW^-1 mod M = b_iU mod M errechnen, sofern M und W bekannt sind.

Gegeben seien nun drei private Schlüssel k_priv1, k_priv2 und k_priv3 mit
 

Gemäß der Formel b_i = a_iW mod M lauten die entsprechenden öffentlichen Schlüssel:
 

Die öffentlichen Schlüssel sind identisch, obwohl drei verschiedene private Schlüssel zur Konstruktion genommen wurden. Für einen öffentlichen Knapsack-Schlüssel B gibt es also nicht nur einen privaten Schlüssel. Wie sich später herausstellen wird, gibt es sogar unendlich viele private Schlüssel.

Jedes Paar (U, M) kann zur Bildung der Menge A herangezogen werden, vorausgesetzt

1. A = (a₁, ...,a_n) mit a_i = b_iU mod M ist superansteigend und
2. a₁ + ... + a_n < M

Der Algorithmus von Shamir zielt darauf ab, aus dem öffentlichen Knapsack-Schlüssel B ein Trapdoor-Paar (U, M) zu ermitteln, so dass die Folge {a_i = b_iU mod M}_i=1...n superansteigend ist. Der Algorithmus läuft in zwei Schritten ab:

1. Suchen kleiner Intervalle in [0, 1[: in einem von diesen Intervallen muss der Quotient U/M liegen
2. Feinere Analyse dieser Intervalle: finden eines Subintervalls, in dem U/M liegt und das Paar (U, M) eine superansteigende Folge erzeugt

Für eine genauere Analyse wird von folgenden Werten ausgegangen:

• a₁ sei eine dn -n bit Zahl
• a_i sei eine dn -n +i -1 bit Zahl
• a_n sei eine dn -1 bit Zahl
• M₀ sei eine dn bit Zahl

Mit den Parametern n = 100 und d = 2 wächst A von 100 bit für a₁ bis zu 199 bit für a₁₀₀.
Der Modulus M₀ ist eine 200 bit Zahl und die einzelnen b_i haben die Größenordung von 200 bit.

Gegeben sei nun ein öffentlicher Knapsack-Schlüssel B = (b₁, ..., b_n). Der unbekannte Modulus sei M₀ und W₀ der unbekannte Multiplikand. Weiterhin sei U₀ = W₀^-1 das Inverse Element zu W₀ (mod M₀).

Schritt 1: Erzeugen kleiner Intervalle in [0, 1[

Gleichzeitig wird der Wertebereich von U erweitert, so dass U reelle Werte annehmen kann. Da U kleiner als M₀ ist, kann U₀ Werte aus dem Intervall [0, M₀[ annehmen. Wird in die Funktion f_i für U der Wert U₀ eingesetzt, erhält man gerade die i-te Komponente von A:

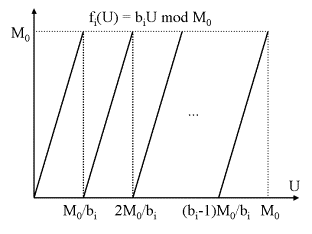
Der Graph der Funktion f_i hat dabei folgendes Aussehen:

• f_i ist eine Sägezahnkurve
• f_i ist stetig bis auf die Nullstellen. Diese liegen bei U = 0, M₀/b_i, 2M₀/b_i, 3M₀/b_i, ... (b_i -1)M₀/b_i
• f_i hat insgesamt b_i Minima in [0, M₀[
• Der Abstand zweier aufeinander folgender Nullstellen beträgt M₀/b_i
• Die Steigung der i-ten Funktion beträgt b_i und ist daher unabhängig von M₀

Analyse der ersten Funktion f₁(U) = b₁U mod M₀:
Da M₀ größer ist als die Summe aller a_i, gilt insbesondere, dass M₀ viel größer ist als a₁. Die Komponente a₁ ist nach Konstruktion eine dn-n bit Zahl. Der (unbekannte) Modulus M₀ ist eine dn bit Zahl. Da b₁ etwa die Größenordung von M₀ hat, ist auch b₁ eine dn bit Zahl.
Der unbekannte Wert U₀ macht gemäß der Formel a₁ = b₁U₀ mod M₀ aus einer dn bit Zahl eine dn-n bit Zahl. Diese Eigenschaft von U₀ schränkt den Bereich ein, in dem U₀ liegen kann.
Die folgende Abbildung versucht zu verdeutlichen, dass U₀ sehr nahe an einer Nullstelle der f₁-Kurve liegen muss. Der Abstand zur nächsten links von U₀ liegenden Nullstelle beträgt nicht mehr als 2^-n.

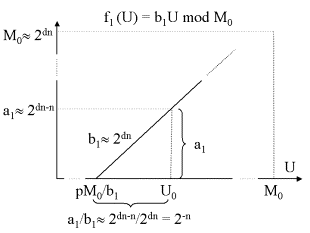
Eine Analyse der zweiten Funktion, f₂(U) = b₂U mod M₀ ergibt ein ähnliches Ergebnis. Da a₂ eine dn-n+1 bit Zahl und b₂ eine dn bit Zahl ist, beträgt der Abstand von U₀ zur nächsten links von U₀ liegenden Nullstelle nicht mehr als 2^-n+1. Auch hier liegt U₀ sehr nahe an einem Minimum.

Da U₀ sehr nahe an einem Minimum der f₁- und f₂-Kurve liegt, folgt, dass diese beiden Nullstellen sehr nahe beieinander liegen. Dabei liegt die Nullstelle der zweiten Kurve höchstens 2^-n+1 links der Nullstelle der f₁-Kurve und höchstens 2^-n rechts von ihr.

Eine Analyse der weiteren Funktionen f₃, f₄, ... ergibt die gleiche Feststellung: der unbekannte Wert U₀ liegt in der Nähe einer Nullstelle dieser Funktionen. Folglich liegen alle diese Nullstellen nahe beieinander.
Anstatt den Wert U₀ zu finden, kann man sich darauf beschränken, Bereiche zu finden, in denen f₁, f₂, f₃, ... eine Nullstelle besitzen. Diese Bereiche werden Anhäufungspunkte (accumulation points) genannt.

Nun stellt sich die Frage, wieviele Funktionen analysiert werden müssen, um eine möglichst geringe Anzahl an Anhäufungspunkten zu erhalten. Dazu sei k die Anzahl der Funktionen, die zu deren Ermittlung genommen werden.
Betrachte das p-te Minimum der f₁-Kurve, gelegen an der Stelle U = pM₀/b₁. Die am nahesten an pM₀/b₁ gelegene Nullstelle der i-ten Funktion liegt irgendwo im Intervall [pM₀/b₁ - M₀/(2b_i), pM₀/b₁ + M₀/(2b_i)], da zwei aufeinander folgende Nullstellen der i-ten Funktion im Abstand M₀/b_i folgen. Angenommen, die Lage der verschiedenen Minima in diesem Intervall sind Zufallsvariablen mit gleicher Wahrscheinlichkeitsverteilung. Dann kann die Wahrscheinlichkeit, dass die Nullstellen der Kurven f₂, f₃, ..., f_k nahe genug am p-ten Minimum der f₁-Kurve liegen, abgeschätzt werden durch 2^-n+1×2^-n+2×...×2^-n+k-1, was in etwa 2^-kn+n+k2/2 entspricht. Da die erste Funktion insgesamt b₁ Minima besitzt, beträgt die erwartete Anzahl an Anhäufungspunkten b₁×2^-kn+n+k2/2, ungefähr 2^dn-kn+n+k2/2.
Dieser Ausdruck wird kleiner als Eins, wenn (k-d-1)n > k²/2. Für große n ist diese Bedingung erfüllt, falls k > d+1. Für d = 2 heisst das, dass nur vier Funktionen betrachtet werden müssen, um nicht zu viele Anhäufungspunkte zu erhalten. Dabei ist d wiederum die Proportionalitätskonstante.

Bevor mit dem Auffinden der Anhäufungspunkte fortgefahren wird, noch eine Beobachtung über die Kurven f_i:
diese Funktionen sind definiert mod M₀. Dieser Wert ist nicht bekannt. Die Positionen der Nullstellen der verschiedenen Funktionen sind aber unabhägnig von M₀. Sie hängen von der Steigung ab. Die Steigung von f_i lautet b_i. Dividiert man daher beide Koordinaten von f_i durch den (unbekannten) Modulus M₀, erhält man n Funktionen f_i(V) = b_iV mod 1. Die Unbekannte in dieser Funktion ist nun V = U/M₀. Der Definitionsbereich ist entsprechend [0, M₀/M₀[ = [0, 1[. Die Steigung der Funktion f_i beträgt b_i. Die Nullstellen liegen nun bei V = 0, 1/b_i, 2/b_i, ..., (b_i -1)/b_i; der Abstand zweier Nullstellen lautet nun 1/b_i.

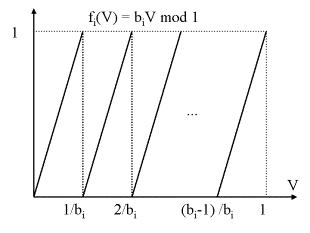
Vor Division durch M₀ betrug der Abstand von U₀ zur nächsten links liegenden Nullstelle der ersten Funktion nicht mehr als 2^-n. Dieser Abstand ist reduziert um M₀ und beträgt nun nicht mehr als 2^{-dn -n}, da M₀ eine dn bit Zahl ist.

Damit nun das p-te Minimum der f₁-Kurve einen Anhäufungspunkt darstellt, müssen in seiner Umgebung Nullstellen von f₂, f₃ und f₄ sein. Das p-te Minimum von f₁ liegt bei V = p/b₁. Die Bedingung, dass die q-te Nullstelle von f₂ um höchstens den Wert d₁ von p/b₁ entfernt liegt, wird durch die Ungleichung

Das Lösen der Ungleichungen ist ein Integer Programming Problem. Solch ein Problem ist polynomiell in der Größe der Koeffizienten lösbar, wenn die Anzahl der Unbekannten fest ist.
Durch Lösen dieser Ungleichungen erhält man Werte für p, so dass

1. p/b₁ ist die p-te Nullstelle von f₁ und
2. in der Nähe von p/b₁ haben f₂, f₃ und f₄ ebenfalls ein Minimum

Schritt 2: Feinere Analyse

Für jeden im Schritt 1 erhaltenen Anhäufungspunkt p wird nun eine genauere Analyse durchgeführt. Dazu werden alle n Funktionen betrachtet. Zum Ermitteln der Anhäufungspunkte wurden nur vier Funktionen berücksichtigt, daher kann es vorkommen, dass ein p-Wert zwar für die ersten vier Kurven einen Anhäufungspunkt darstellt, jedoch nicht für die übrigen Funktionen.

Sei nun p ein Anhäufungspunkt, im Schritt 1 erhalten. Betrachtet wird jetzt das Intervall [p/b₁, (p+1)/b₁[, das Intervall zweier aufeinander folgender Nullstellen der f₁-Kurve.

Für das Intervall [p/b₁, (p+1)/b₁[ werden nun die Nullstellen aller Funktionen f₂, f₃, ..., f_n ermittelt. Diese Nullstellen werden aufsteigend nach dem v-Wert sortiert.
Sei {v₁, v₂, ..., v_s} die Liste aller Nullstellen in [p/b₁, (p+1)/b₁[. Innerhalb eines Intervalls [v_j, v_j+1[ gibt es, bis auf v_j selbst, keine weiteren Nullstellen. Jede Funktion f_i kann daher in diesem Intervall als Geradengleichung ausgedrückt werden:

Die folgende Abbildung zeigt, wie sich die Funktion f_i zwischen Nullstellen als Geradengleichung beschreiben lässt. Im ersten Intervall [0, 1/b_i[ heisst die Gleichung f_i(V) = b_iV. Im nächsten Intervall [1/b_i, 2/b_i[ wird der T-Wert erhöht, da f_i in [0, 2/b_i[ genau einmal modulo 1 reduziert wurde. In [1/b_i, 2/b_i[ lautet die Darstellung f_i(V) = b_iV -1. In [2/b_i, 3/b_i[ wurde zweimal modulo 1 reduziert: f_i = b_iV -2. Auf diese Weise lässt sich f_i in jedem Intervall zwischen zwei aufeinander folgenden Nullstellen eindeutig als Geradengleichung darstellen.

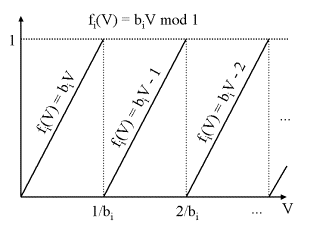
Untersucht wird nun, ob in [v_j, v_j+1[ ein Subintervall existiert, so dass die Funktionen in diesem Subintervall superansteigend sind und zudem ihre Summe < 1 ist. Wichtig ist, dass V in das Intervall [v_j, v_j+1[ eingeschränkt wird, da nur in einem solchen Intervall jede Funktion eindeutig als Geradengleichung beschrieben werden kann.
Für n Funktionen erhält man n-1 Ungleichungen in der Unbekannten V, um die superansteigende Eigenschaft zu erfüllen.

Die erste Ungleichung, f₂(V) > f₁(V) <=> b₂V - T_{2, j} > b₁V - T_{1, j}, aufgelöst nach V, ergibt zum Beispiel

• V > (T_{2, j} - T_{1, j})/(b₂ - b₁), falls b₂ > b₁
• V < (T_{2, j} - T_{1, j})/(b₂ - b₁), falls b₂ < b₁

• ]MAX(V, v_j), v_j+1[, falls V > (T_{2, j} - T_{1, j})/(b₂ - b₁)
• [v_j, MIN(V, v_j+1[, falls V < (T_{2, j} - T_{1, j})/(b₂ - b₁):

Die Summe aller Funktionen ist kleiner als Eins für

Nach Auswerten aller Ungleichungen sind in [v_j, v_j+1[ die Bedingunen möglicherweise nicht erfüllbar und es ist ein in [v_j, v_j+1[ leeres Unterintervall entstanden. In diesem Fall wird das nächste Intervall [v_j+1, v_j+2[ untersucht. Dabei ändert sich genau ein T-Wert. Der T-Wert der Funktion, die an der Stelle v_j+1 ein Minimum besitzt, wird um Eins erhöht, da die entsprechende Funktion in ]0, v_j+1] nun eine Nullstelle mehr hat. Alle anderen T-Werte bleiben unverändert.

Sei nun ]u_l, u_r[ das nicht-leere Subintervall, welches nach Auswerten aller Bedingungen erhalten wurde. Für jedes V aus ]u_l, u_r[ und für alle Funktionen f_i gilt:

1. f_i(V) > f₁(V) + ... + f_i-1(V) und
2. f₁(V) + ... + f_n(V) < 1

Sei nun p/q eine rationale Zahl aus ]u_l, u_r[. Es gilt:

• f_i(p/q) > f₁(p/q) + ... + f_i-1(p/q)
• f₁(p/q) + ... + f_n(p/q) < 1

• f_i(p) > f₁ + ... + f_i-1(p)
• f₁(p) + ... + f_n(p) < q

Applet starten

 

DES