4.5.5 Shamirs algorithm

Recall, how a Merkle-Hellman key-pair is generated:
Choose a superincreasing sequence A = (a₁, ..., a_n), a modulus M with M > a₁ + ... + a_n and a multiplier W with 1 <= W < M. Additionally, W must be relative prim to M, i.e. gcd(M, W) = 1. This choice of W guarantees an inverse element U, such that UW = 1 (mod M). M, W and the set A constitutes the private key, whereas the public key is the set of integers B = (b₁, ..., b_n), with b_i = a_iW mod M.

Provided, M and W are given, the components a_i may be computed by a_i = b_iW^-1 mod M = b_iU mod M.

Get the corresponding public keys by computing b_i = a_iW mod M. The public keys are
 

The keys k_pub1, k_pub2 and k_pub3 are indentical, though three different private keys were used. Obviously, there are many private keys producing the same public key. Indeed, as will turn out later, there are infinetely many private keys corresponding to a public key.

Every pair (U, M) can be used to get the (secret) set A, provided that

1. A = (a₁, ...,a_n) with a_i = b_iU mod M is a superincreasing sequence and
2. a₁ + ... + a_n < M

The aim of the presented algorithm is to compute a trapdoor pair, such that the resulting set A = {a_i = b_iU mod M}_i=1...n is a superincreasing one. The algorithm is divided into two parts:

1. find few small intervals in [0, 1[: in one of those intervals the ratio U/M must be
2. carry out a finer analysis: find a subinterval such that U/M is in this subinterval and (U, M) produces a superincreasing sequence.

To make the analysis easier, the following values are used:

• a₁ is a dn -n bit number
• a_i is a dn -n +i -1 bit number
• a_n is a dn -1 bit number
• M₀ is a dn bit number

Setting n = 100 and d = 2, the components of A increase in size from 100 bits for a₁ up to 199 bits for a₁₀₀.
The modulus M then is a 200 bit number.

Given a public key B = (b₁, ..., b_n). Let M₀ be the (unknown) modulus and W₀ the (unknown) multitplier used to construct the public key B. The inverse element to W is denoted by U₀.

Part one: Get a few small intervals in [0, 1[

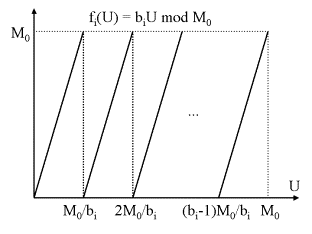
Consider arbitrary real positive values for U. As U is less than M₀, the functions are defined in [0, M₀[. For U = U₀, function i produces exactly a_i:

The graph of function i is as follows:

• f_i has a sawtooth form
• The minima of f_i are located at U = 0, M₀/b_i, 2M₀/b_i, 3M₀/b_i, ... (b_i -1)M₀/b_i
• f_i has a total of b_i minima in [0, M₀[
• the distance between two successive minima is M₀/b_i
• the slope is b_i

Now analyze f₁(U) = b₁U mod M₀:
The modulus M₀ is greater than the sum of all a_i. So M₀ is much bigger than a₁.
The integer a₁ is a dn-n bit number, M₀ a dn bit number as is b₁. So the unknown U₀ transforms a dn bit number to a dn-n bit number. The following image tries to make clear, that the unknown U₀ must be located near a minima of the first function. The distance to the next left minima is less than 2^-n.

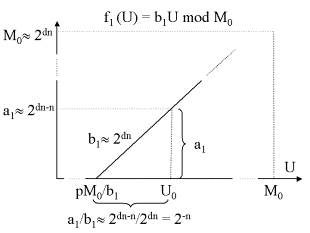
Doing the same analysis with funcion f₂, the result is the same. The unknown U₀ is again near a minima of the second function. As a₂ is a dn-n+1 bit number, U₀ transforms a dn bit number to a dn-n+1 bit number. For that reason, U₀ is located at most 2^-n+1 right of a minimum of function two.

Since U₀ is located near a minimum of f₁ as well as f₂, there are minima of f₁ and f₂ being very close to another. The minimum of f₂ is at most 2^-n+1 to the left and at most 2^-n to the right of the minimum of f₁.

The same analysis holds for f₃, f₄, ...
U₀ is located near a minimum of all these functions, so the minima are very close to each other. The problem of finding U₀ itself can be reformulated as the problem of finding accumulation points of minima of the various functions.

Let k be the number of functions, used to get the accumulation points. Consider the p-th minimum of f₁, located at U = pM₀/b₁. The nearest minimum of f_i to pM₀/b₁ is in the interval [pM₀/b₁ - M₀/(2b_i)], because the distance of two successive minima of f_i is M₀/b_i. Assume now, that the minima in [pM₀/b₁ - M₀/(2b_i)] are random variables with uniform probability distributions. Then the probability, that the mimima of f₂, ..., f_k are sufficiently close the p-th minimum of function one, can be estimated by 2^-n+1×2^-n+2×...×2^-n+k+1, which is about 2^-kn+n+k2/2. As there are b₁ different minima of f₁, the expected number of accumulation points is b₁×2^-n+1×2^-n+2×...×2^-n+k+1, which is about 2^dn-kn+n+k2/2. This expression is less than 1, if (k-d-1)n > k²/2. If n is large, this expression is true, if k > d+1. Using d=2, only 4 functions have to be analyzed for getting accumulation points in number not too much. Here, d is again the proportionality constant.

But prior to computing the accumulation points, one problem remains: the functions are defined modulo M₀. This number is unknown. The minima of the i-th function depend on the slope, which is b_i. By dividing both coordinates of the i-th function by M₀, new functions f_i are definded as follows: f_i(V) = b_iV mod 1, with the new variable V in [0, 1[. The slope still is b_i and the number of minima remains b_i. The locations of the minima are now at V = 0, 1/b_i, 2/b_i, ..., (b_i-1)/b_i and the distance of two minima is reduced to 2^-dn-n, because M₀ is a dn bit number.

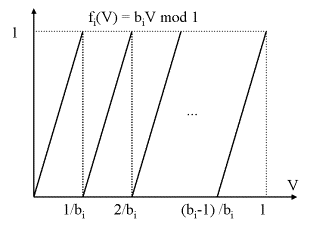
The unknown value V₀ now is at most 2^-dn-n right to a minimum of function f₁.

To get the accumulation points, consider the p-th minimum of f₁, located at p/b₁. To be an accumulation point, there have to be minima of f₂, f₃ and f₄ near p/b₁. The q-th minimum of f₂ is at V = q/b₂, the r-th minimum of f₃ at V = r/b₃ and the s-th minimum of f₄ is at V = s/b₄. So all these minima must be close to p/b₁. Expressed as a formula, this means that

By mulitplying with the denominators, the follwing equivalent system of inequalities is obtained:

This is an integer programmming problem. Lenstra has showed, that this can be solved in polynomial time in the size of the coefficients, if the number of variables is fixed.

With solving this system of inequalites, numbers p are computed for which

1. p/b₁ is the p-th minimum of f₁ and
2. near p/b₁ there are also minima of f₂, f₃ and f₄

Part two: carry out a finer analysis

With the end of step one, all accumulation points, satisfying the inequalities are found. For each of these accumulation points, perform a finer analysis. Consider now all n functions. To obtain the accumulation points, only four functions were used. For that reason, you might get points, f₂, f₃ and f₄ have a close minimum to it, but not all the other functions.

Now let p be an accumulation point. Consider the interval [p/b₁, (p+1)/b₁[, which is the interval of two successive minima of function f₁.

For this interval, get all the minima of all functions and sort them in increasing order by the v-coordinate.
Let {v₁, v₂, ..., v_s} be the list of all minima in [p/b₁, (p+1)/b₁[. The only minimum in [v_j, v_j+1[ is located at v_j, so every function f_i may be described as a linear segment:

The following image explains the fact, that within two minima, function i may be written as a linear segment. Within ]0, 1/b_i[, no minima exist. In the next interval, f_i is exactly once reduced modulo 1, so the T-value is increased and is now 1. The line segment in [1/b_i, 2/b_i[ may be written as f_i = b_iV - 1, V in [1/b_i, 2/b_i[. Turning to [2/b_i, 3/b_i[, the segment is now f_i = b_iV mod 2, because a further minimum exists at V = 2/b_i. So between two neighbouring minima, f_i may be written as a line segment.

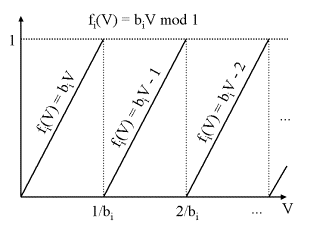
The task is now to scan every interval [v_j, v_j+1[, if there exists a subinterval satisfying the supericreasing property and in which the sum of all functions is less than one. It is important to limit the value V into [v_j, v_j+1[. Only in such an interval, all functions can be written in the form f_i = b_iV - T_{i, j}.
Because there are n functions, there are n-1 inequalities. All of these inequalities have to be evaluated to satisfy the superincreasing property. For example, to satisfy the condition that f₂ is greater than f₁, V is limited by

• V > (T_{2, j} - T_{1, j})/(b₂ - b₁), if b₂ > b₁
• V < (T_{2, j} - T_{1, j})/(b₂ - b₁), if b₂ < b₁

• ]MAX(V, v_j), v_j+1[, if V > (T_{2, j} - T_{1, j})/(b₂ - b₁)
• ]v_j, MIN(V, v_j+1)[, if V < (T_{2, j} - T_{1, j})/(b₂ - b₁)

As stated above, if one inequality is not satisfiable in [v_j, v_j+1[, turn to the next interval [v_j+1, v_j+2[ and try again. Exactly one T-value changes, namely the T-value of that function having a minima at v_j+1. This value is increased by one. All other values remain unchanged.

Now suppose, the resulting interval is nonempty. Let ]u_l, u_r[ be that interval. For every V in ]u_l, u_r[, all functions f_i satisfy

1. f_i(V) > f₁(V) + ... + f_i-1(V) and
2. f₁(V) + ... + f_n(V) < 1

Let p/q be an arbitrary rational number in ]u_l, u_r[. The following holsd true

• f_i(p/q) > f₁(p/q) + ... + f_i-1(p/q)
• f₁(p/q) + ... + f_n(p/q) < 1

• f_i(p) > f₁ + ... + f_i-1(p)
• f₁(p) + ... + f_n(p) < q

Start applet

 

DES