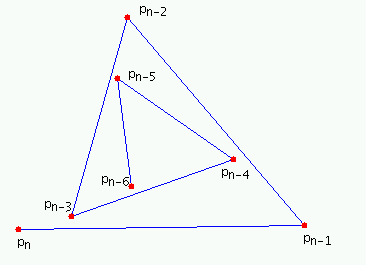
Theorem 2
Let T={p1-p2-...-pn}
for odd n>2 have the shape of a spiral
numbered from inside to outside.
Then we need at least (n-1)(n-2)/2
edge slides to get a tree
containing the edge (pn-2,pn).